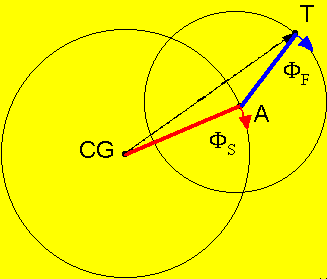

The simple two arms model adequatly describes the yawing motion of spin-stabilized bullets, resulting from the action of all aerodynamic moments.
The yawing motion can be understood as a superposition of a fast and a slow oscillation, often called nutation and precession.
Imagine to look at the bullet from the rear. The slow mode arm CG to A should be hinged at the CG and rotates with the slow mode frequency. Consequently A moves on a circle around the CG (the red circle). The fast mode arm A to T, where T is the bulletīs tip, should be hinged at A and rotates with the fast mode frequency. Thus, T rotates on a circle about A. CG to T is the projection of the bulletīs longitudinal axis.
An animation of the two arms model is shown in the figure below.
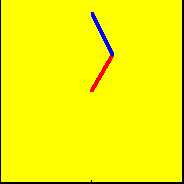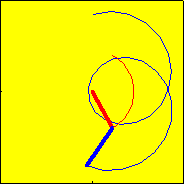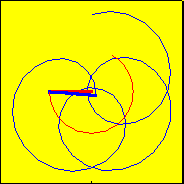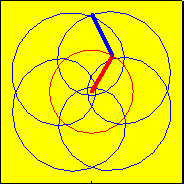
One additionally has to consider that the fast mode frequency exceeds the slow mode frequency (which is true in the animation) and the arm lengths CG to A and A to T are continuously shortened (which is not true in the animation) if the bullet is dynamically stable.