The drag coefficient

The drag coefficient cD is the most important aerodynamic coefficient and generally depends on

- bullet geometry (symbolic variable B),
- Mach number Ma,
- Reynolds number Re,
- the angle of yaw d

The following assumptions and simplifications are usually made in ballistics:

1. Re neglection

It can be shown, that with the exception of very low velocities, the Re dependency of c_D can be neglected.

2. d dependency

Depending on the physical ballistic model applied, an angle of yaw is either completely neglected (d=0) or only small angles of yaw are considered. Large angles of yaw are an indication of instability.
For small angles of yaw the following approximation is usually made:

a) c_D(B,Ma,d) = c_Do(B,Ma) + c_Dd(B,Ma) * d²/2

Another theory which accounts for arbitrary angles of yaw is called the "crossflow analogy prediction method". A discussion of this method is far beyond the scope of this article, however the general type of equation for the drag coefficient is as follows:

b) c_D(B,Ma,d) = c_Do(B,Ma) + F(B,Ma,Re,d)

3. Determination of the zero-yaw drag coefficient

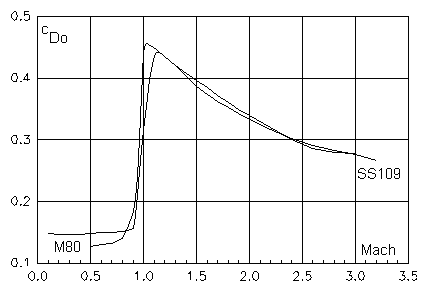
The zero-yaw drag coefficient as a function of the Mach number Ma is generally determined experimentally either by wind tunnel tests or from Doppler Radar measurements.

Fig.: Zero-yaw drag coefficient for two military bullets
M80 (cal. 7.62 x 51 Nato)
SS109 (cal. 5.56 x 45)

There is also software available which estimates the zero-yaw drag coefficient as a function of the Mach number from bullet geometry. The latter method is mainly applied in the development phase of a new projectile.

4. Standard drag functions

Generally each bullet geometry has its own zero-yaw drag coefficient as a function of the Mach number. This means, that specific - time-consuming and expensive - measurements would be required for each bullet geometry. A widely used simplification makes use of a "standard drag function" c_Do^standard which depends on the Mach number alone and a form factor i_D which depends on the bullet geometry alone according to:

c_Do(B,Ma) = i_D(B) * c_Do^standard(Ma)

If this simplification is applicable, the determination of the drag coefficient of a bullet as a function of the Mach number is reduced to the determination of a suitable form factor alone. It will be shown that the concept of the ballistic coefficient, widely used in the US for small arms projectiles follows this idea.

Abbreviations