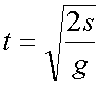
However, while falling, the drag of both objects will be very small, and they will "approximately" hit the ground at the same time.
2. For bullets fired from handguns through the atmosphere, the maximum range (typically in the range of a few kilometres or less) is usually reached for a 30°- 35° departure angle. This is a consequence of bullet retardation by the drag force.
3. Artillery shells may reach maximum ranges of a few dozens of kilometres. When fired at higher departure angles, theseprojectiles are capable to reach much higher altitudes than handgun bullets.However in those altitudes the air density is considerably smaller than the ground air density. Lower air density goes along with lower drag and this is the reason why artillery shells reach their maximum range for higher angles of departure (typically at 45°).
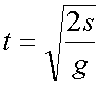
A: This is an interesting question and the answer is not trivial.
It is true that the horizontally fired bullet and the dropped bullet would hit the surface at the same moment, if the experiment happens in vacuum. In vacuum there is only the force of gravity which affects both objects in the same way.
However if the shooting occurs in air there is the additional force of drag.
Both objects - let us assume spheres - experience drag. The difference however is, that the horizontally fired bullet has a much higher velocity. Only the "downward" velocity components vy at t=0 are the same (vy=0) for both bullets.
The force of drag is (roughly) proportional to the square of the velocity v (v = sqrt(vx2 + vy2)) and not only to the vy component! Thus, the drag experienced by the fired bullet is much higher than the drag experienced by the dropped bullet. As a consequence the fired bullet will reach the surface later.
Example: Sphere of 10 mm diameter, 10 g mass, fired at 500 m/s from 10 m height
1. Horizontally fired: flight time 1.649 s; terminal velocity 160.2 m/s; point of impact at approx. X = 400 m (range)
2. Dropped: fall time 1.432 s, terminal velocity 13.9 m/s
Q: Centrifugal force is a ficticious force, it does not exist! There is only a force radially inward which is the centripetal force.
It would be interesting to ask NASA for a verification!
Please also read that Internet source! It seems that the Soviets already thought about using guns in outer space!
This would be a second experiment for NASA!
A: The answer depends on the type of gun.
Typically bullets fired from pistols and revolvers travel at 300 - 500 m/s.
Hunting or miltary bullets are faster (approx. 800 - 1000 m/s).
Air rifles are in the 100 - 200 m/s range.
![]()
![]()
Q: What is the unit
of the drag coefficient cD and what is the connection between
cD and the projectile caliber?
A:The drag coefficient is a dimensionless number (in the area of 0.1 - 1) and
depends on Mach number, Reynolds Number, Froude number,...
The drag coefficient is usually measured by Doppler Radar or other velocity
loss measurements. There is no simple relationship between bullet geometry (length, diameter,
shape) and cD.
A: All the aerodynamic coefficients are usually hard to obtain. Military research institutes measure them but only for military bullets. Almost no data is available for bullets from the civilian market. There is some (expensive) software available which estimates the aerodynamic coefficients from bullet geometry.
A: This question is hard to answer in general. The best I can give is a "worst-case" estimation.
When a gun is fired vertically, the bullet after some time reaches a summit where the velocity is zero, and then falls back. The bullet will fall back base first which is hard to calculate. I can estimate the velocity if it would fall nose first, that is the normal flying position for which drag is well known - so the real terminal velocity will actually be smaller than the following prediction.
- For a .22 lr bullet (m=40 grain, v0 = 1150 ft/s)
the summit will be at 1164 ft, the total flight time 30 seconds and the terminal velocity 270 ft/s
- For a SS109 military bullet (m= 55 grain, v0=3200 ft/s)
the summit will be at 2650 ft, the total flight time 44 seconds and the terminal velocity 404 ft/s.
For this bullet are indications that it will become unstable. This will further reduce summit height and terminal velocity considerably.
A: This is not an easy task and can only be done with some accuracy by applying exterior ballistics software. There is a simple formula for estimation purposes.
z = k1*T2
T is the total flight time in seconds
k1 is a factor in the area of 0,1 ... 0,12 m/s2 which depends on spin, muzzle velocity and bullet parameters
z is the side deviation in metersGenerally bullet drift at short distances (100 - 300 yd) is by far smaller than the normal scatter.
Drift is only of some practical importance for artillery shells, at ranges of several miles.
A: The most important (and expensive part) of the equipment will be a light source -
a spark flash of very small flash time (in the area of 1 millionth of a second).
This is something you do not get in the supermarket.